TEST #12 : Nouvelles mesures avec la bobine v1.1 et la nouvelle plaque à induction

TEST #12 : Nouvelles mesures avec la bobine v1.1 et la nouvelle plaque à induction
créé le 28 décembre 2012 - JLN Labs - Mis à jour le 16 Janvier 2013
All informations and diagrams are published freely (freeware) and are intended for a private use and a non commercial use.
Toutes les informations et schémas sont publiés gratuitement ( freeware ) et sont destinés à un usage personnel et non commercial

15 janvier 2013 - TEST #12 : Ceci est la suite des tests de la bobine v1.1 avec une nouvelle plaque à induction de marque "Rosenstein & Söhne" de référence NC-3050. Dans ce test la puissance a été limitée au niveau 5/10, c'est à dire à mi-puissance (environ 1200W).

Il est très appréciable, avec ce modèle de plaque à induction, de ne pas avoir besoin d'une plaque métallique ferromagnétique pour initialiser l'allumage des lampes halogènes.

Dans ce test j'ai connecté en sortie de la bobine bifilaire plate de Tesla, les charges suivantes :

La PUISSANCE TOTALE des charges connectées en SORTIE du GEGENE est de 3550 Watts

Pour les mesures de la tension et du courant produits à la sortie et alimentant les lampes halogènes de charge, les deux sondes de l'oscilloscope sont utilisées sur le calibre X10 et connectées à la sortie de la bobine plate bifilaire. La sonde Ch1 mesure la tension AC aux bornes de la bobine plate bifilaire et la sonde Ch2 donne le courant en mesurant la tension aux bornes d'une résistance non inductive Mundorf MR10 de 0.1 ohm 10W. La puissance d'entrée est mesurée sur le secteur à l'aide d'un Wattmètre Energy Logger 4000F.

Les valeurs des tensions True RMS sur le Ch1 et Ch2 sont calculées en temps réel par l'oscilloscope numérique Rigol...

La puissance électrique d'alimentation de la plaque à induction est mesurée à l'aide d'un Wattmètre Energy Logger 4000F directement connecté sur le secteur :

Le Wattmètre mesure 1165 Watt à l'entrée de l'alimentation de la plaque à induction.

Ci-dessus les valeurs des Tensions True RMS mesurées par les sondes de l'oscilloscope numérique Rigol.

Afin d'avoir une bonne précision des valeurs mesurées pour le calcul mathématique, la fréquence d'échantillonnage est réglée à 20.00 MSa/s

Voici les données de l'oscilloscope numérique traitées et calculées sous GNU Octave 3.2.4 (version libre et compatible de MATLAB)

Voici le code source de mon programme utilisé pour le traitement des données de l'oscilloscope Rigol et qui fonctionne sur Octave 3.2.4 ou Matlab R7 ou plus

% GEGENE Project - RMS Voltage, Current and Power calculator
% by Jean-Louis Naudin - January 15, 2013
% www.jlnlab.com
%
% This program runs on OCTAVE Version 3.2.4 or MATHLAB r7.0 or more
% GNU General Public Licence - this is a freeware
%
% v1.01 : add the trapeze method calculation
%
clear all; close all; clc

r=0.09; % Current probe resistance value in Ohm

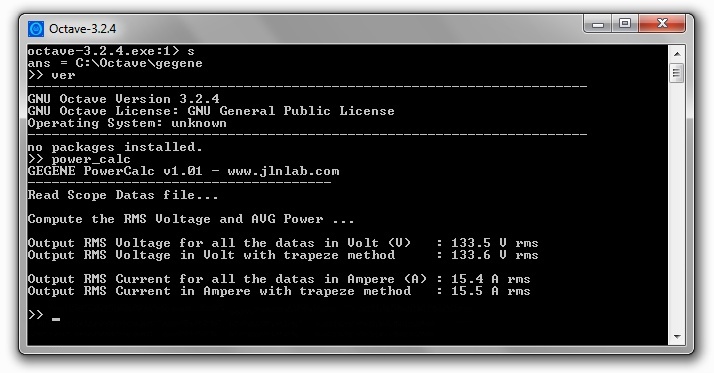
fprintf('GEGENE PowerCalc v1.01 - www.jlnlab.com\n');
fprintf('--------------------------------------\nRead Scope Datas file...\n\n');

datas = dlmread('NewFile0.csv', ',',2,0); % read the datas scope file
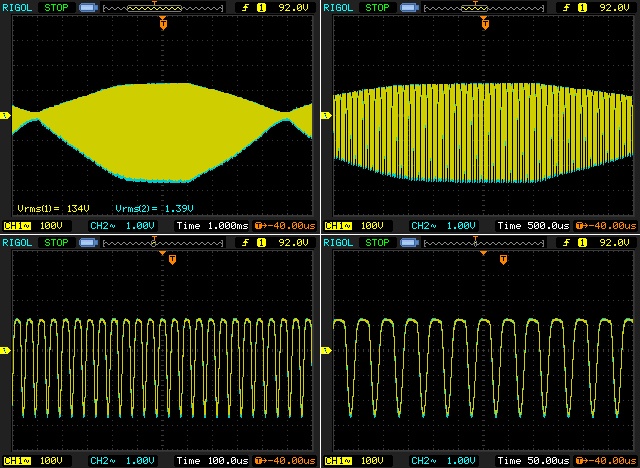
% Below a sample of the CSV datas from the Rigol digital oscilloscope
% X,CH1,CH2,
% Second,Volt,Volt,
% -3.72e-03,8.40e+01,7.60e-01,
% -3.70e-03,-3.20e+01,-3.60e-01,
% -3.68e-03,-2.80e+01,-2.80e-01,

l=length(datas); % numbers of sample
t=datas(1:l,1); % t: time base
u1=datas(1:l,2); % ch1: voltage output
u2=datas(1:l,3); % ch2: voltage accros the current probe

%
% compute the RMS Voltage
%
fprintf('Compute the RMS Voltage and AVG Power ...\n\n');
%VTG_rms=norm(u1)/sqrt(length(u1));
VTG_rms = sqrt(sum(u1.*conj(u1))/size(u1,1));
veff=sqrt(trapz(t,u1.*u1)/(t(l)-t(1)));
vrms = zeros(l,1);
vrms = vrms + VTG_rms;
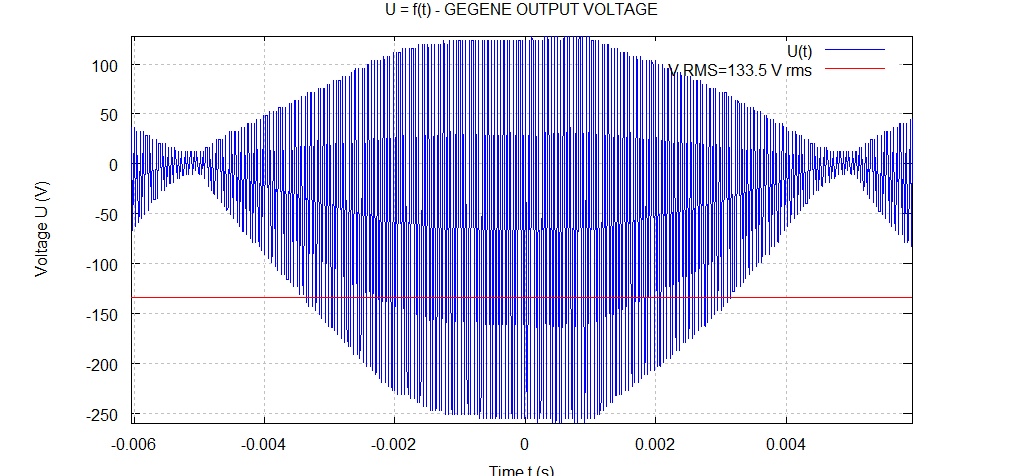
figure(1); clf;
plot(t,u1,'-b',t,vrms,'-r',t,-vrms,'-r');
xlabel('Time t (s)');
ylabel('Voltage U (V)');
title('U = f(t) - GEGENE OUTPUT VOLTAGE');
axis([t(1) t(l) min(u1) max(u1)]);
disp(['Output RMS Voltage for all the datas in Volt (V) : ',sprintf('%0.1f',VTG_rms),' V rms']);
disp(['Output RMS Voltage in Volt with trapeze method : ',sprintf('%0.1f',veff),' V rms']);
grid on
legend('U(t)',['V RMS=',sprintf('%0.1f',VTG_rms),' V rms']);

%
% compute the RMS Current
%
ip2=u2/r;
%CUR_rms=norm(u2/r)/sqrt(length(u2));
CUR_rms = sqrt(sum(u2/r.*conj(u2/r))/size(u2/r,1));
ceff=sqrt(trapz(t,ip2.*ip2)/(t(l)-t(1)));
crms = zeros(l,1);
crms = crms + CUR_rms;
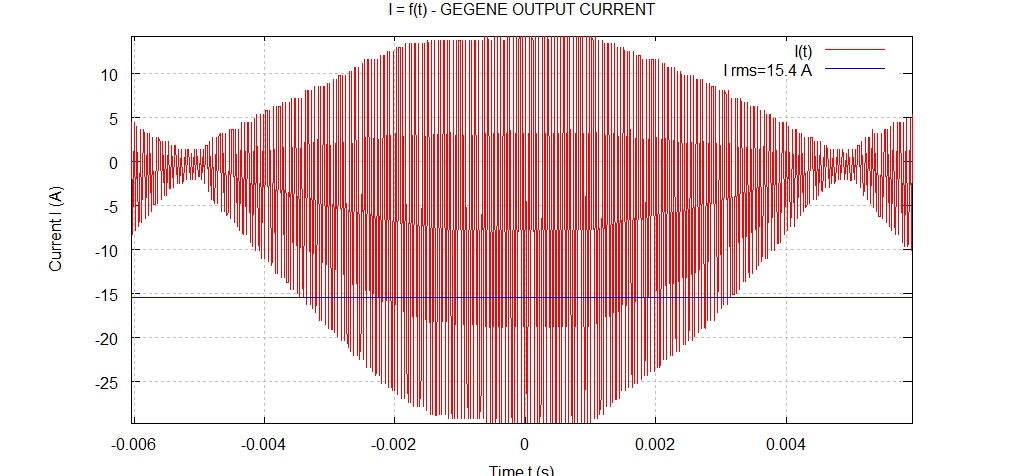
figure(2); clf;
plot(t,ip2,'-r',t,crms,'-b',t,-crms,'-b');
xlabel('Time t (s)');
ylabel('Current I (A)');
title('I = f(t) - GEGENE OUTPUT CURRENT');
axis([t(1) t(l) min(ip2) max(ip2)]);
disp(['Output RMS Current for all the datas in Ampere (A) : ',sprintf('%0.1f',CUR_rms),' A rms']);
disp(['Output RMS Current in Ampere with trapeze method : ',sprintf('%0.1f',ceff),' A rms']);
grid on
legend('I(t)',['I rms=',sprintf('%0.1f',CUR_rms),' A']);

%
% compute the Average Power
%
pp=u1.*u2/r;
Pavg = VTG_rms * CUR_rms;
pmoy=trapz(t,pp)/(t(l)-t(1));
pwravg = zeros(l,1);
pwravg = pwravg + Pavg;
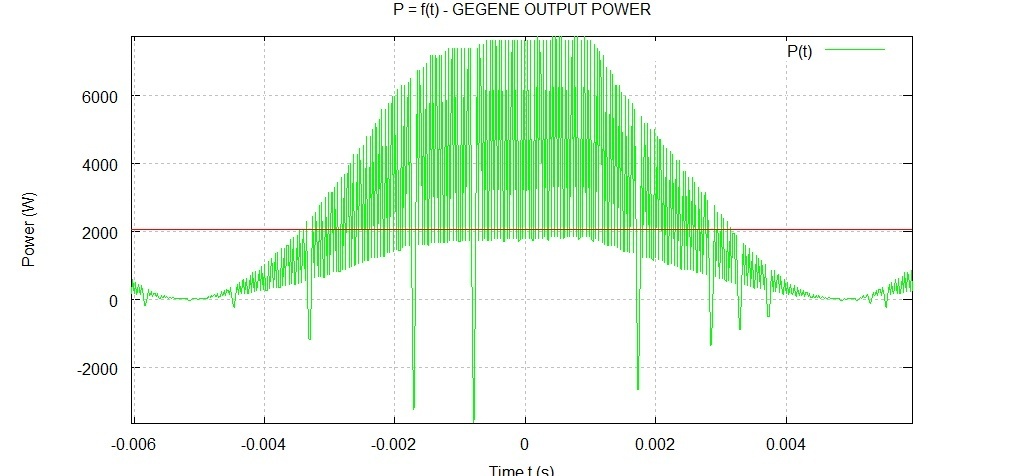
figure(3); clf;
plot(t,pp,'-g',t,pwravg,'-r');
xlabel('Time t (s)');
ylabel('Power (W)');
title('P = f(t) - GEGENE OUTPUT POWER');
axis([t(1) t(l) min(pp) max(pp)]);
disp(['---> OUTPUT AVG Power (VTG_rms * CUR_rms): ',sprintf('%0.1f',Pavg),' Watt ']);
disp(['---> OUTPUT AVG Power (Trapeze method) : ',sprintf('%0.1f',pmoy),' Watts']);
grid on
legend('U(t)',['AVG PWR =',sprintf('%0.1f',Pavg),' W ']);